In making this guide I wanted to try to answer the question that has always accompanied me in the struggle for freedom of choice: "What is herd immunity".

The doubts that accompanied me were not born on the web, or rather, they were not born from buffalo sites but from sites and institutional communications such as the 2017-19 vaccination plan of the Ministry of Health which reads a long series of advantages of the "vaccination " among which:

"The benefit is therefore direct, deriving from the vaccination itself which immunizes the vaccinated person totally or partially, and indirectly, by virtue of the creation of a safety net, in favor of the non-vaccinated subjects, which reduces the risk of contagion. The extraordinary nature of the instrument is given by the fact that it, in the face of a modest use of resources, entails these significant benefits in terms of individual immunity and collective immunity (herd immunity)". ¹

Wow, what crazy villain wouldn't get vaccinated for all the existing vaccines? Well, but are we sure that everything is how it is sold to us?

Herd immunity theory

According to the herd immunity theory, the spread of an infection can be stopped when a large number of people are immune and the higher the percentage of individuals immunized, the less likely it is that an individual will come into contact with the pathogen. Simple, concise, effective, but is it so linear?

On a hypothetical level absolutely yes, the more you immunize and the less likely you are that that certain pathogen will spread but, while this concept is possible, always hypothetically, the threshold established by the models is absolutely not demonstrated in practice, nor is it shown that in our societies a decrease in the percentage of vaccinated subjects automatically leads to the cancellation of the herd effect, therefore we are in the field of theories and the concept of herd immunity is a theoretical concept.

The concept of herd immunity is scientifically known ², what is less known is the fact that in the original description of herd immunity, protection for the general population occurs only if people have contracted natural infection and the reason is quite trivial, the naturally contracted disease generates immunity for life.

Let's go back to the definition "for Dummies" of flock immunity: the more the population is immunized and the less likely it is that the pathogen will spread, only hypothetically because it is not demonstrated in practice today that this occurs: the concept is originally defined on the basis of naturally contracted disease, which gives immunity for life.

Over time, those who support vaccination as the supreme solution have used the term "flock immunity", linking it to vaccinations, that is, vaccine-induced immunity. The big problem with this theory is the duration - limited in time - of vaccine-induced immunization, a known fact. Furthermore, the possible lack or reduced response of the immune response depends both on individual factors - genetic or temporary alterations of the functionality of the immune system, pathologies or therapeutic treatments that cause immunosuppression - and on factors related to the way the vaccine interacts with the immune system ( responsible for an intrinsically low efficacy).
In addition, the need to administer multiple booster shots to allow for an adequate antibody response increases the risk of improperly stimulating the immune system and can lead to autoimmune, hyperimmunization or immunosuppression.
But more concretely, as well-known professors repeat the concept of herd immunity to us on unified TV, any parent who has vaccinated their children and tries to do antibody titrations will easily understand how much the "big problem" gets bigger than expected. An unexpected and worrying number of vaccinated subjects, even recently, has no induced immunity. Do you want proof? Do antibody titrations to your vaccinated children. Rivaccinateli according to calendar, do the antibody tests. Well, now do it on 100, 1.000 and 10.000 subjects and then bring the evidence that the non-responders, the scientifically proven subjects that should not respond to vaccinations, are only 5%.

The concepts of vaccination and herd immunity hardly meet, they run aground lonely in distant beaches called "real life": these vaccines, and probably the vaccine as it has always been conceived, can lead to poor, very scarce induced immunity , and with a short if not very short duration.

Let's go back to the definition "for Dummies" of flock immunity and add a little bit: the more the population is immunized and the less likely there is that the pathogen will spread, all hypothetically because it has not been demonstrated in practice today that this happens: originally the concept based on naturally contracted disease, which gives immunity for life. Vaccine-induced immunity, despite being the commonly recognized mantra, does not take into account the real efficacy of some vaccines both as an immunization and as a duration of immunization.

That's enough? No, the vaccinocentric vision needs more evidence to support the thesis "let's vaccinate the stones" and if the evidence isn't there, well, it creates confusion. Among the concepts on which it has deliberately created confusion are "flock immunity" and "flock effect". ³ We have understood herd immunity, I hope, but basically this concept concerns immunized subjects while herd effect concerns the remaining non-immunized. Let's explain it more clearly: if we put 95% of the immunized population (both vaccine-induced and natural disease) as herd immunity, we are talking about those who have been immunized, but if we talk about "herd effect" we are talking about those, the 5% in this example, not immunized or immunizable.

The flock effect, to be more precise, is defined as: "the reduction of infection or disease in the unvaccinated segment as a result of immunization of a proportion of the population". The herd effect, to be analyzed separately from herd immunity also using the vaccinocentric vision, can be measured by quantifying the decrease in the incidence of an infection used as a parameter on the unvaccinated segment of a population in which an immunization program is established. So if it is true that a public health program induces or enhances herd immunity, it is not said that it also causes a decrease in the likelihood of getting sick in the unvaccinated or vaccinated. Let's remember it, we are in the field of pure theory.

And now a little bit of algebra and vaccination

If we examine the theory on which flock immunity is based, in a very simplified way, herd immunity (herd immunity) is an equation that essentially depends on the contagiousness of each disease. ^4-5 The contagiousness of diseases is defined as R₀ (Reproductive rates of the infectious agent) which theoretically determines how many people an infected patient can on average infect.
For the Dummies: a pathogen with R₀= 2 has a prediction of 2 infected for each infected. If the R.₀ is 20 you will have 20 infections each infected, and so on.

Let's go back to us, to calculate herd immunity we will have to make a simple equation (H sta Herd Immunity):

H = 1- (1 / R₀)

I wish the passage was clear, those good at math will excuse me, I will use R₀ higher, that of measles, as an example and I will do all the steps:

H = 1 - (1 / R0) applied to measles will be H = 1 - (1/18)

therefore H = 1 - (1/18) becomes H = 1 - 0,055555555555556 or H = 0,944444444444444 which rounded down does 0,94. The R₀ measles is 94%.

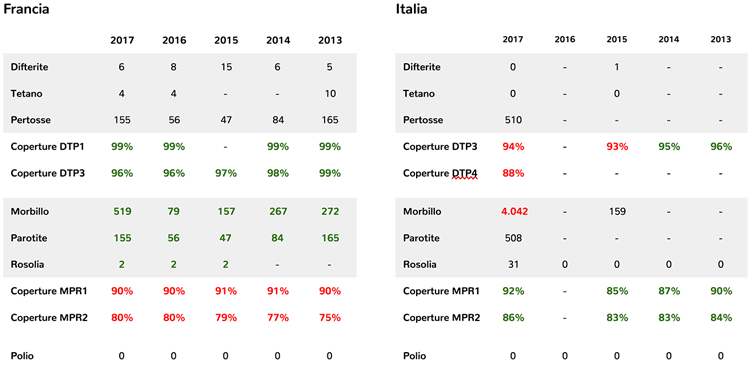
Obviously we know what R is₀ of all diseases that can have contagiousness and from this derives the following scheme, which we copied from the scientific publications mentioned below:

I would be imprecise if I did not speak of the new generation matrix, introduced by Prof. Diekmann to calculate R₀ ⁷. Just think about it, I leave you the deepening, which in the new models for calculating the R₀ new variants enter, among which the R1 and the R2, the subdivision in more classes of population, for example a population whose R₀ in a normal community it is of a certain factor, the same R in the hospital would increase factor for the quantity of pathogens and the greater possibility of being exposed to the pathogen considered.
For ordinary citizens, parents like me, one concept must be clear: R₀ low do not determine the danger of the pathogen, R₀= 1.8 (therefore significantly lower than a 5-7 associated with Rubella) of the Ebola epidemic in the Congo (1995) or that with an R₀= 1.34 of the Ebola epidemic of 2000 in Uganda, make us understand how both group immunity and the R factor₀ are influenced by other factors in health policy choices, far less simple than a mathematical formula.

Let's go back to the definition "for Dummies" of flock immunity and add a little bit: the more the population is immunized and the less likely there is that the pathogen will spread, all hypothetically because it has not been demonstrated in practice today that this happens: originally the concept based on naturally contracted disease, which gives immunity for life. Vaccine-induced immunity, despite being the commonly recognized mantra, does not take into account the real efficacy of some vaccines both as an immunization and as a duration of immunization. Lastly, however, according to the mathematical formula for determining herd immunity, we are (already before 2017) well above the immunity thresholds of almost all diseases, therefore the emergency becomes even less real.

But in real life, all this math is needed?

Well friends, when I was a child I always asked my teacher what mathematics was for and never once I received a comprehensive answer and today, in reality to the immunity of flocks, everything becomes even more mysterious.
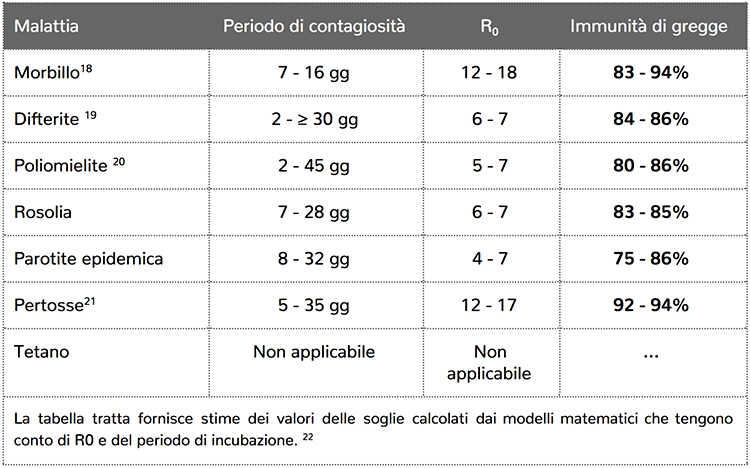
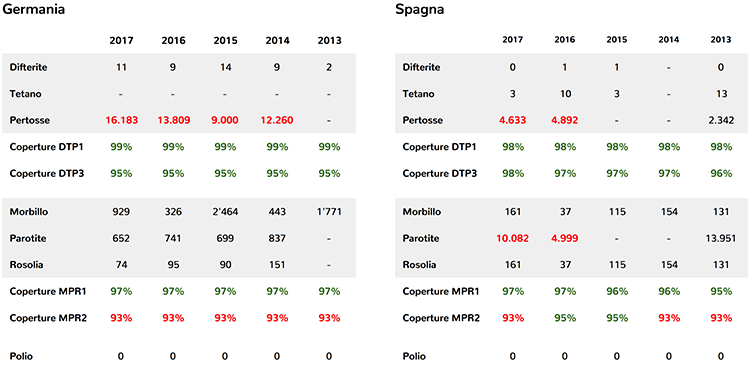
If you analyze the following data, taken from the World Health Organization website ⁸, we understand that vaccination coverage is not related to epidemic outbreaks in various states.
Countries with hexavalent coverage greater than ours, such as Germany, have cases of diphtheria every year, a disease apparently eradicated by us. Countries like Spain that see good coverage for MPR (measles-mumps-rubella vaccine) have very few problems with measles but mumps epidemic cycles with 10.000 cases per year in 2017. France, which has seen compulsory vaccinations increased from 2018 to 3 since 10, has always had vaccination coverage below 80% but has NEVER had epidemic cycles of exanthematous diseases. The mystery deepens on Germany which sees from 2014 to 2017 on average 11.000 cases of whooping cough per year, with vaccination coverage DTP1 (first dose of difetrite-tetanus-pertussis vaccine) over 99% and DTP3 (third dose of the same vaccine) at 95% therefore above 1 percentage point to that famous calculation in the table a little more above, referring to whooping cough.

Source:
http://apps.who.int/immunization_monitoring/globalsummary/countries?countrycriteria%5Bcountry%5D%5B%5D=ESP
http://apps.who.int/immunization_monitoring/globalsummary/countries?countrycriteria%5Bcountry%5D%5B%5D=DEU

Source: 
http://apps.who.int/immunization_monitoring/globalsummary/countries?countrycriteria%5Bcountry%5D%5B%5D=FRA
http://apps.who.int/immunization_monitoring/globalsummary/countries?countrycriteria%5Bcountry%5D%5B%5D=ITA

Let's go back to the definition "for Dummies" of herd immunity and let's simplify it: Herd immunity is a theory, period. The rest is pseudoscience valid perhaps for mental exercises. The vaccine-induced herd immunity theory is annually denied by reality. end

1. National vaccination plan 2017-2019 pag 42-82 - http://www.salute.gov.it/imgs/C_17_pubblicazioni_2571_allegato.pdf
2. P. Fox, L. Elveback, W. Scott, L. Gatewood, and E. Ackerman, Herd immunity: basic concept and relevance to public health immunization practices, Am. J Epidemiol., 94 (1971), pp. 179-189
E. Fine, Herd immunity: history, theory, practice, Epidemiol. Rev., 15 (1993), pp. 265-30
3. TJ John and R. Samuel, Herd immunity and herd effect: new insights and definitions, Eur. J Epidemiol., 16 (2000), pp. 601-606
4. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2249331/pdf/epidinfect00010-0010.pdf pg. 8
5. https://academic.oup.com/cid/article/52/7/911/299077/Herd-Immunity-A-Rough-Guide
6. Paul EM FINE. Herd immunity: history, theory, practice. Epidemiol. Rev. 1993. 15; 2: 265-302)
7. 18. Heffernan JM, Smith RJ, Wahl LM. Perspectives on the basic reproductive ratio. R Soc Pub. 2005; 2 (4): 281-93. [PMC free articles] [PubMed]
8. http://apps.who.int/immunization_monitoring/globalsummary/timeseries/tsincidencemeasles.html